(本小题满分13分)如图,在四棱锥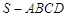 中,底面
中,底面 是正方形,
是正方形, 底面
底面 ,
, , 点
, 点 是
是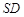 的中点,
的中点, ,且交
,且交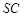 于点
于点 .
.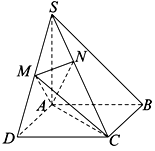
(Ⅰ)求证: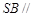 平面
平面 ;
;
(Ⅱ)求证:直线 平面
平面 ;
;
(Ⅲ)求直线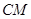 与平面
与平面 所成角的余弦值.
所成角的余弦值.
已知直线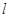 :
: 与圆C:
与圆C: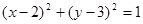 相交于
相交于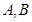 两点.
两点.
(Ⅰ)求弦 的中点
的中点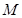 的轨迹方程;
的轨迹方程;
(Ⅱ)若 为坐标原点,
为坐标原点,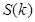 表示
表示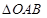 的面积,
的面积, ,求
,求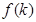 的最大值.
的最大值.
将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连结EB、FB、FA后围成一个空间几何体如图2所示,
(1)求异面直线BD与EF所成角的大小;
(2)求二面角D—BF—E的大小;
(3)求这个几何体的体积.
在等比数列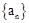 中,
中,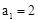 ,
, 。
。
(Ⅰ)求数列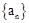 的通项公式;
的通项公式;
(Ⅱ)令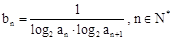 ,求数列
,求数列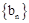 的前n项和
的前n项和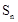 。
。
在ΔABC中,内角A,B,C所对的边分别为a,b,c,已知 .
.
(1) 求 的值; (2) 若
的值; (2) 若 是钝角,求sinB的取值范围
是钝角,求sinB的取值范围
已知: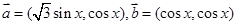 ,
,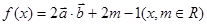
(1)求 关于
关于 的表达式,并求
的表达式,并求 的最小正周期;
的最小正周期;
(2)若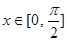 时
时 的最小值为5,求
的最小值为5,求 的值.
的值.