(1)如图中图(1),已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD.请你完成图形,并证明:BE=CD.(尺规作图,不写作法,保留作图痕迹)
(2)如图(2),已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD.BE与CD有什么数量关系?简单说明理由.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图(3),要测量池塘两岸相对的两点B,E间的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.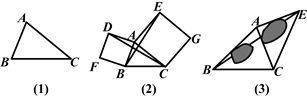
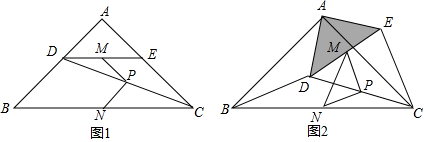
如图1,在 中, , ,点 , 分别在边 , 上, ,连接 ,点 , , 分别为 , , 的中点.
(1)观察猜想:图1中,线段 与 的数量关系是 ,位置关系是 ;
(2)探究证明:把 绕点 逆时针方向旋转到图2的位置,连接 , , ,判断 的形状,并说明理由;
(3)拓展延伸:把 绕点 在平面内自由旋转,若 , ,请直接写出 面积的最大值.
学校“百变魔方”社团准备购买 , 两种魔方,已知购买2个 种魔方和6个 种魔方共需130元,购买3个 种魔方和4个 种魔方所需款数相同.
(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买 , 两种魔方共100个(其中 种魔方不超过50个).某商店有两种优惠活动,如图所示.请根据以上信息,说明选择哪种优惠活动购买魔方更实惠.

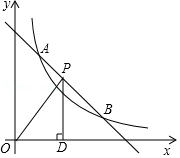
如图,一次函数 与反比例函数 的图象交于点 和 .
(1)填空:一次函数的解析式为 ,反比例函数的解析式为 ;
(2)点 是线段 上一点,过点 作 轴于点 ,连接 ,若 的面积为 ,求 的取值范围.
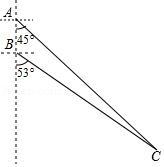
如图所示,我国两艘海监船 , 在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 ,此时, 船在 船的正南方向5海里处, 船测得渔船 在其南偏东 方向, 船测得渔船 在其南偏东 方向,已知 船的航速为30海里 小时, 船的航速为25海里 小时,问 船至少要等待多长时间才能得到救援?(参考数据: , , ,
如图,在 中, ,以 为直径的 交 边于点 ,过点 作 ,与过点 的切线交于点 ,连接 .
(1)求证: ;
(2)若 , ,求 的长.
