甲与乙两人掷硬币,甲用一枚硬币掷3次,记下国徽面朝上的次数为m;乙用一枚硬币掷2次,记下国徽面朝上的次数为n.
(1)算国徽面朝上不同次数的概率并填入下表:
(2)现规定:若m>n,则甲胜;若n≥m,则乙胜.你认为这种规定合理吗?为什么?
已知曲线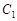 的极坐标方程为
的极坐标方程为 ,曲线
,曲线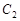 的极坐标方程为
的极坐标方程为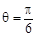 ,曲线
,曲线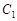 、
、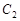 相交于
相交于 、
、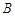 两点. (
两点. (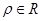 )
)
(Ⅰ)求 、
、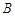 两点的极坐标;
两点的极坐标;
(Ⅱ)曲线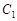 与直线
与直线 (
(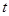 为参数)分别相交于
为参数)分别相交于 两点,求线段
两点,求线段 的长度.
的长度.
如图,已知圆 与圆
与圆 外切于点
外切于点 ,直线
,直线 是两圆的外公切线,分别与两圆相切于
是两圆的外公切线,分别与两圆相切于 两点,
两点, 是圆
是圆 的直径,过
的直径,过 作圆
作圆 的切线,切点为
的切线,切点为 .
.
(Ⅰ)求证: 三点共线;
三点共线;
(Ⅱ)求证: .
.
已知两点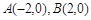 ,直线AM、BM相交于点M,且这两条直线的斜率之积为
,直线AM、BM相交于点M,且这两条直线的斜率之积为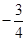 .
.
(Ⅰ)求点M的轨迹方程;
(Ⅱ)记点M的轨迹为曲线C,曲线C上在第一象限的点P的横坐标为1,直线PE、PF与圆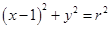 (
( )相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
)相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
求△OQR的面积的最大值(其中点O为坐标原点).
已知函数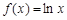 ,
,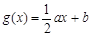 .
.
(Ⅰ)若 与
与 在
在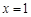 处相切,试求
处相切,试求 的表达式;
的表达式;
(Ⅱ)若 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(Ⅲ)证明不等式: 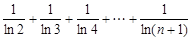
 .
.
四棱锥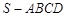 ,底面
,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面 .已知
.已知 ,
, ,
,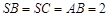 ,
, 为线段
为线段 的中点.
的中点.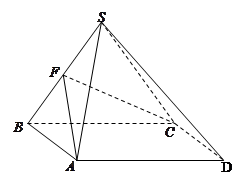
(Ⅰ)求证: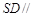 平面
平面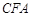 ;
;
(Ⅱ)证明: .
.