(本小题满分12分)已知函数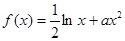
 .
.
(1)若曲线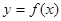 在点
在点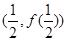 处的切线
处的切线 与直线
与直线 :
: 垂直,求
垂直,求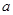 的值;
的值;
(2)讨论函数 的单调性;若存在极值点
的单调性;若存在极值点 ,求实数
,求实数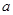 的取值范围.
的取值范围.
求函数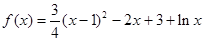 在区间[1,3]上的极值。
在区间[1,3]上的极值。
在平面直角坐标系xOy中,曲线C1的参数方程为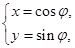 (
(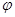 为参数)曲线C2的参数方程为
为参数)曲线C2的参数方程为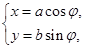 (
(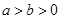 ,
,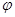 为参数)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=
为参数)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=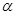 与C1,C2各有一个交点.当
与C1,C2各有一个交点.当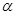 =0时,这两个交点间的距离为2,当
=0时,这两个交点间的距离为2,当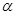 =
=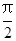 时,这两个交点重合.
时,这两个交点重合.
(I)分别说明C1,C2是什么曲线,并求出a与b的值;
(II)设当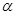 =
= 时,l与C1,C2的交点分别为A1,B1,当
时,l与C1,C2的交点分别为A1,B1,当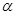 =-
=- 时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.
(Ⅰ)当a=-2时,求不等式f(x)<g(x)的解集;
(Ⅱ)设a>-1,且当x∈[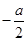 ,
,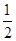 )时,f(x)≤g(x),求a的取值范围.
)时,f(x)≤g(x),求a的取值范围.
在平面直角坐标系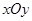 中,求过椭圆
中,求过椭圆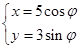 (
(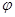 为参数)的右焦点且与直线
为参数)的右焦点且与直线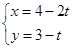 (
( 为参数)平行的直线的普通方程。
为参数)平行的直线的普通方程。
设不等式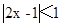 的解集为M.
的解集为M.
(I)求集合M;
(II)若a,b∈M,试比较ab+1与a+b的大小.