(本小题满分13分)已知椭圆 过点
过点 ,且与抛物线
,且与抛物线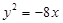 有一个公共的焦点.
有一个公共的焦点.
(Ⅰ)求椭圆 方程;
方程;
(Ⅱ)斜率为 的直线
的直线 过椭圆
过椭圆 的右焦点
的右焦点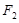 ,且与椭圆交于
,且与椭圆交于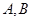 两点,求弦
两点,求弦 的长;
的长;
(Ⅲ)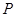 为直线
为直线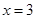 上的一点,在第(Ⅱ)题的条件下,若△
上的一点,在第(Ⅱ)题的条件下,若△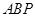 为等边三角形,求直线
为等边三角形,求直线 的方程.
的方程.
已知函数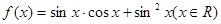 .
.
(1)求函数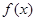 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)若角A是锐角三角形的一个内角,求 的取值范围.
的取值范围.
已知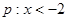 或
或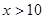 ;
;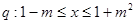 ;
; 是
是 的充分而不必要条件,求实数
的充分而不必要条件,求实数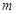 的取值范围.
的取值范围.
. 已知函数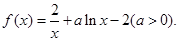
(1)若曲线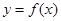 在点
在点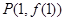 处的切线与直线
处的切线与直线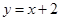 垂直,求函数
垂直,求函数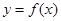 的单调区间;
的单调区间;
(2)若对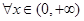 都有
都有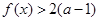 成立,试求实数a的取值范围;
成立,试求实数a的取值范围;
(3)记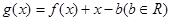 ,当a=1时,函数
,当a=1时,函数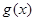 在区间
在区间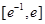 上有两个零点,求实数b的取值范围.
上有两个零点,求实数b的取值范围.
(本小题满分12分)某公司生产陶瓷,根据历年的情况可知,生产陶瓷每天的固定成本为14000元,每生产一件产品,成本增加210元.已知该产品的日销售量 与产量
与产量 之间的关系为
之间的关系为 , 每件产品的售价
, 每件产品的售价 与产品
与产品 之间的关系为
之间的关系为
(I)写出该陶瓷厂的日销售利润 与产量
与产量 之间的关系式;
之间的关系式;
(II)若要使得日销售利润最大,每天该生产多少件产品,并求出最大利润.
(本小题满分12分) 中,
中, 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知 满足
满足 ,且
,且
(1)求角A的大小;
(2)求 的值
的值