(本小题满分10分)选修4-1 :几何证明选讲
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且DE2 = EF·EC.
(Ⅰ)求证:CE·EB = EF·EP;
(Ⅱ)若CE:BE = 3:2,DE = 3,EF = 2,求PA的长.
(选修4-4不等式选讲)
已知x,y,z均为正数.求证: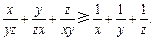
已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 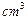 .
.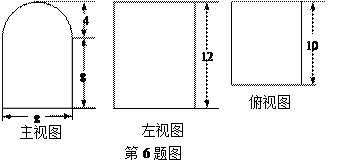
(选做题)选修4-1:几何证明选讲
如图,AB是⊙O的直径,D是 的中点,DE⊥AC交AC的延长线于点F.
的中点,DE⊥AC交AC的延长线于点F.
⑴求证:DE是⊙O的切线;
⑵若 DE="3" ,⊙O的半径为5,求BF的长。
(本小题满分18分)已知数列{an}、{bn}、{cn}的通项公式满足bn=an+1-an,cn=bn+1-bn(n∈N*),若数列{bn}是一个非零常数列,则称数列{an}是一阶等差数列;若数列{cn}是一个非零常数列,则称数列{an}是二阶等差数列(1)试写出满足条件a1=1,b1=1,cn=1(n∈N*)的二阶等差数列{an}的前五项;(2)求满足条件(1)的二阶等差数列{an}的通项公式an;(3)若数列{an}首项a1=2,且满足cn-bn+1+3an=-2n+1(n∈N*),求数列{an}的通项公式
(本小题满分16分)通过研究学生的学习行为,心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间:讲授开始时,学生的兴趣激增;中间有一段不太长的时间,学生的兴趣保持较理想的状态;随后学生的注意力开始分散.分析结果和实验表明,用f(x)表示学生掌握和接受概念的能力(f(x)的值越大,表示接受的能力越强),x表示提出和讲授概念的时间(单位:min),可有以下的公式: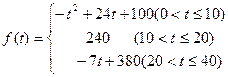
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?