如图,四边形ABCD中,AB=CD,G,H分别是BC,AD的中点,BA,CD的延长线分别交GH的延长线于点E,F.猜想∠AEH与∠F的关系,并说明理由.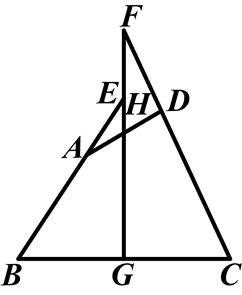
(1)先化简,再求值: ,其中x=2015.
,其中x=2015.
(2)如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点O落在水平面上,对称轴是水平线OC,点A、B在抛物线造型上,且点A到水平面的距离AC=4米,点B到水平面的距离为2米,OC=8米.
①请建立适当的直角坐标系,求抛物线的函数解析式;(需要画出你建立的直角坐标系)
②为了安全美观,现需要在水平线OC上找一点P,用质地、规格已确定的圆形钢管制作两根支柱PA、PB对抛物线造型进行支撑加固,那么怎样才能找到两根支柱用料最省时的点P?请写出找法.(无需证明)(支柱与地面、造型对接方式的用料多少问题暂不考虑)
将边长为8cm的正方形纸片ABCD沿EG折叠(折痕EG分别与AB、DC交于点E、G),使点B落在AD边上的点 F处,FN与DC交于点M,连接BF与EG交于点P.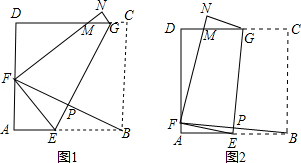
(1)当点F与AD的中点重合时(如图1):
①△AEF的边AE= cm,EF= cm,线段EG与BF的大小关系是EG BF;(填“>”、“=”或“<”)
②求△FDM的周长.
(2)当点F在AD边上除点A、D外的任意位置时(如图2):
③试问第(1)题中线段EG与BF的大小关系是否发生变化?请证明你的结论;
④当点F在何位置时,四边形AEGD的面积S最大?最大值是多少?
甲、乙两车从A地前往B地,甲车行至AB的中点C处后,以原来速度的1.5倍继续行驶,在整个行程中,汽车离开A地的距离y与时刻t的对应关系如图所示,求:
(1)甲车何时到达C地;
(2)甲车离开A地的距离y与时刻t的函数解析式;
(3)乙车出发后何时与甲车相距20km.
如图1,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.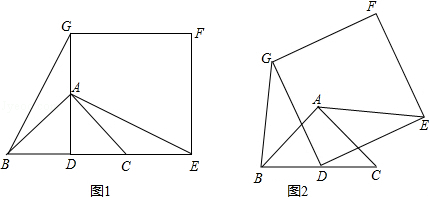
(1)试猜想线段BG和AE的数量关系是 ;
(2)将正方形DEFG绕点D逆时针方向旋转α(0°<α≤360°),
①判断(1)中的结论是否仍然成立?请利用图2证明你的结论;
②若BC=DE=4,当AE取最大值时,求AF的值.
在平面直角坐标系xOy中,抛物线y=mx2-2mx-2(m≠0)与y轴交于点A,其对称轴与x轴交于点B.
(1)求点A,B的坐标;
(2)设直线l与直线AB关于该抛物线的对称轴对称,求直线l的解析式;
(3)若该抛物线在-2<x<-1这一段位于直线l的上方,并且在2<x<3这一段位于直线AB的下方,求该抛物线的解析式.