(本小题满分12分)已知椭圆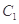 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为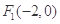 ,
,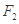
 ,点
,点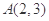 在椭圆
在椭圆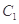 上,过点
上,过点 的直线
的直线 与抛物线
与抛物线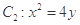 交于
交于 两点,抛物线
两点,抛物线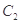 在点
在点 处的切线分别为
处的切线分别为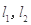 ,且
,且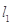 与
与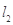 交于点
交于点 .
.
(Ⅰ)求椭圆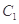 的方程;
的方程;
(Ⅱ)是否存在满足 的点
的点 ? 若存在,指出这样的点
? 若存在,指出这样的点 有几个(不必求出点
有几个(不必求出点 的坐标);若不存在,说明理由.
的坐标);若不存在,说明理由.
佛山某学校的场室统一使用“佛山照明”的一种灯管,已知这种灯管使用寿命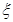 (单位:月)服从正态分布
(单位:月)服从正态分布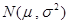 ,且使用寿命不少于
,且使用寿命不少于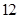 个月的概率为
个月的概率为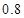 ,使用寿命不少于
,使用寿命不少于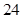 个月的概率为
个月的概率为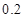 .
.
(1)求这种灯管的平均使用寿命 ;
;
(2)假设一间功能室一次性换上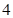 支这种新灯管,使用
支这种新灯管,使用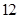 个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少两支灯管需要更换的概率.
个月时进行一次检查,将已经损坏的灯管换下(中途不更换),求至少两支灯管需要更换的概率.
如图,三棱锥 中,
中, 底面
底面 ,
,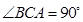 ,
, ,
,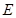 为
为 的中点,点
的中点,点 在
在 上,且
上,且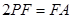 .
.
(1)求证:平面 平面
平面 ;
;
(2)求平面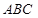 与平面
与平面 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值.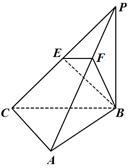
在△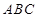 中,角
中,角 、
、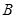 、
、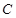 的对边分别为
的对边分别为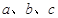 ,满足
,满足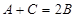 ,且
,且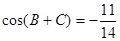 .
.
(1)求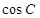 的值;
的值;
(2)若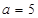 ,求△
,求△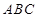 的面积.
的面积.
已知函数 ,
,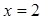 是
是 的一个极值点.
的一个极值点.
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)当 时,求方程
时,求方程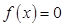 的解的个数.
的解的个数.
已知椭圆的两焦点为 ,
, ,离心率
,离心率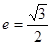 .
.
(1)求此椭圆的方程;
(2)设直线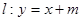 ,若
,若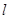 与此椭圆相交于
与此椭圆相交于
 ,
,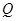 两点,且
两点,且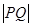 等于椭圆的短轴长,求
等于椭圆的短轴长,求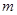 的值;
的值;