已知抛物线 .
(1)当 时,求抛物线与 轴的交点坐标及对称轴;
(2)①试说明无论 为何值,抛物线 一定经过两个定点,并求出这两个定点的坐标;
②将抛物线 沿这两个定点所在直线翻折,得到抛物线 ,直接写出 的表达式;
(3)若(2)中抛物线 的顶点到 轴的距离为2,求 的值.

如图1, 的直径 , 是弦 上一动点(与点 , 不重合), ,过点 作 交 于点 .
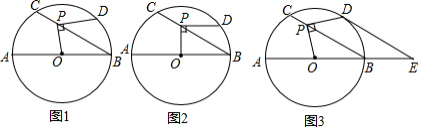
(1)如图2,当 时,求 的长;
(2)如图3,当 时,延长 至点 ,使 ,连接 .
①求证: 是 的切线;
②求 的长.
如图,直线 与双曲线 相交于点 .已知点 , ,连接 ,将 沿 方向平移,使点 移动到点 ,得到△ .过点 作 轴交双曲线于点 .
(1)求 与 的值;
(2)求直线 的表达式;
(3)直接写出线段 扫过的面积.

如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为 ,双层部分的长度为 ,经测量,得到如下数据:
|
单层部分的长度 |
|
4 |
6 |
8 |
10 |
|
150 |
|
双层部分的长度 |
|
73 |
72 |
71 |
|
(1)根据表中数据的规律,完成以下表格,并直接写出 关于 的函数解析式;
(2)根据小敏的身高和习惯,挎带的长度为 时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为 ,求 的取值范围.

为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
|
种类 |
|
|
|
|
|
|
出行方式 |
共享单车 |
步行 |
公交车 |
的士 |
私家车 |
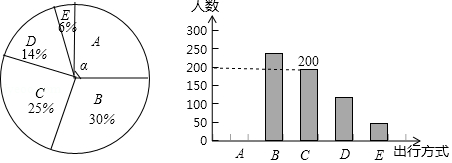
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择 类的人数有 人;
(2)在扇形统计图中,求 类对应扇形圆心角 的度数,并补全条形统计图;
(3)该市约有12万人出行,若将 , , 这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.