请观察下列算式,找出规律并填空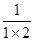 =1-
=1-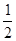 ,
, 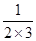 =
=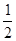 -
-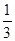 ,
, 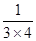 =
=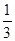 -
-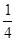 ,
, 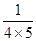 =
=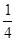 -
-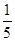 则:
则:
(1)第10个算式是 = .
(2)第n个算式为 = .
(3)根据以上规律解答下题: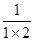 +
+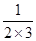 +
+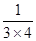 + … +
+ … +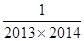 的值.
的值.
某中学为了了解本校学生喜爱的球类运动,在本校范围内随机调查了部分学生,将收集的数据绘制成如下两幅不完整的统计图.请你根据图中提供的信息解答下列问题:
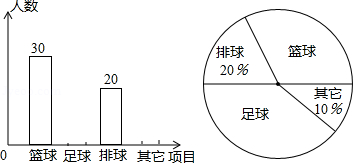
(1)本次一共调查了多少名学生?
(2)补全条形统计图;
(3)求“足球”在扇形统计图中所占圆心角的度数;
(4)若已知该校有500名学生,请你根据调查的结果估计爱好“足球”和“排球”的学生共有多少人?
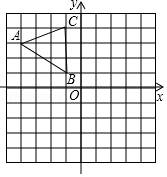
在平面直角坐标系中, 的位置如图所示.(每个小方格都是边长为1个单位长度的正方形)
(1)画出 关于 轴对称的△ ;
(2)将 绕点 逆时针旋转 ,画出旋转后得到的△ ,并直接写出此过程中线段 扫过图形的面积(结果保留
在平面直角坐标系 中, 抛物线 的开口向上, 且经过点
(1) 若此抛物线经过点 ,且与 轴相交于点 , .
①填空: (用 含 的代数式表示) ;
②当 的值最小时, 求抛物线的解析式;
(2) 若 ,当 ,抛物线上的点到 轴距离的最大值为 3 时, 求 的值 .
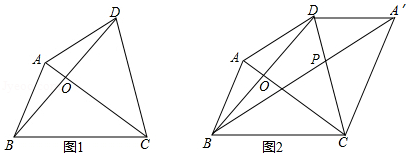
如图1,四边形 的对角线 , 相交于点 , , , , , .
(1)填空: 与 的数量关系为 ;
(2)求 的值;
(3)将 沿 翻折,得到△ (如图 ,连接 ,与 相交于点 .若 ,求 的长.
如图,在 中, , , ,点 , 分别在 , 上(点 与点 , 不重合),且 ,将 绕点 逆时针旋转 得到△ .当△ 的斜边、直角边与 分别相交于点 , (点 与点 不重合)时,设 , .
(1)求证: ;
(2)求 关于 的函数解析式,并直接写出自变量 的取值范围.
