【原创】选修4-2:矩阵与变换(本小题满分10分)
设二阶矩阵 ,
, 满足
满足 ,
, ,求
,求 ..
..
(本小题满分14分)
某工厂生产一种产品的成本费共由三部分组成:①原材料费每件50元;②职工工资支出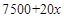 元;③电力与机器保养等费用为
元;③电力与机器保养等费用为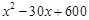 元.其中
元.其中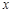 是该厂生产这种产品的总件数。
是该厂生产这种产品的总件数。
(1)把每件产品的成本费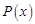 (元)表示成产品件数
(元)表示成产品件数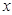 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量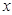 不超过170件且能全部销售,根据市场调查,每件产品的销售价为
不超过170件且能全部销售,根据市场调查,每件产品的销售价为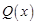 (元),且
(元),且 ,试问生产多少件产品,总利润最高?并求出最高总利润。(总利润=总销售额-总的成本)
,试问生产多少件产品,总利润最高?并求出最高总利润。(总利润=总销售额-总的成本)
(本小题满分14分)
如图,在四棱锥E—ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,求证:
(1) AE∥平面BDF;
(2) 平面BDF⊥平面BCE.
(本小题满分14分)
如图,O为坐标原点,点A,B在⊙O上,且点A在第一象限,点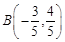 ,点C为⊙O与
,点C为⊙O与 轴正半轴的交点,设∠COB=θ.
轴正半轴的交点,设∠COB=θ.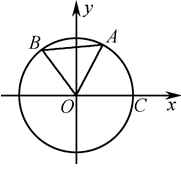
(1) 求sin2θ的值;
(2) 若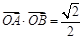 ,求点A的横坐标xA.
,求点A的横坐标xA.
设 ,
,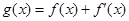 .
.
(1)求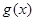 的单调区间和最小值;
的单调区间和最小值;
(2)讨论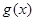 与
与 的大小关系;
的大小关系;
(3)求 的取值范围,使得
的取值范围,使得 <
<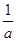 对任意
对任意 >0成立
>0成立
:已知函数 .
.
(Ⅰ)若 ,令函数
,令函数 ,求函数
,求函数 在
在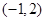 上的极大值、极小值;
上的极大值、极小值;
(Ⅱ)若函数 在
在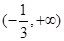 上恒为单调递增函数,求实数
上恒为单调递增函数,求实数 的取值范围.
的取值范围.