已知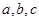 都是正数,求证:
都是正数,求证: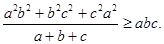
如图,在正三棱锥 中, , .

(1)若 的中点为 , 的中点为 ,求 与 的夹角;
(2)求 的体积.
在 中,内角 所对的边分别为 .已知 , .
(Ⅰ)求 的值;
(Ⅱ)求 的值.
已知函数 .
(Ⅰ)求曲线 的斜率为1的切线方程;
(Ⅱ)当 时,求证: ;
(Ⅲ)设 ,记 在区间 上的最大值为 ,当 最小时,求 的值.
已知椭圆 的右焦点为 ,且经过点 .
(Ⅰ)求椭圆 C的方程;
(Ⅱ)设 O为原点,直线 与椭圆 C交于两个不同点 P, Q,直线 与 x轴交于点 M,直线 与 x轴交于点 N,若 ,求证:直线 l经过定点.
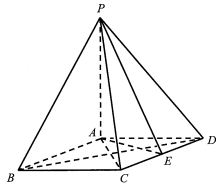
如图,在四棱锥 中, ,底部 ABCD为菱形, E为 CD的中点.
(Ⅰ)求证: ;
(Ⅱ)若 ,求证: ;
(Ⅲ)棱 PB上是否存在点 F,使得 ?说明理由.