如图，直线与轴交于A点，与反比例函数的图象交于点M，过M作M-优题课

如图，直线与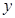轴交于A点，与反比例函数的图象交于点M，过M作MH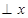轴于点H，且tan∠AHO=2．

（1）求k的值，
（2）点N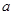（，l）是反比例函数图象上的点，在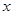轴上是否存在点P，使得PM+PN最小?若存在，求出点P的坐标；若不存在，请说明理由．

科目数学题型解答题难度中等

知识点：平行线分线段成比例一次函数的最值

如图，抛物线 $y = a x^{2} + bx - 4$ 经过 $A (- 3, 0)$ ， $B (5, - 4)$ 两点，与 $y$ 轴交于点 $C$ ，连接 $AB$ ， $AC$ ， $BC$ ．

（1）求抛物线的表达式；

（2）求证： $AB$ 平分 $∠ CAO$ ；

（3）抛物线的对称轴上是否存在点 $M$ ，使得 $ΔABM$ 是以 $AB$ 为直角边的直角三角形，若存在，求出点 $M$ 的坐标；若不存在，请说明理由．

如图， $AB$ 为 $⊙ O$ 的直径， $C$ 为 $⊙ O$ 上一点， $D$ 为 $BA$ 延长线上一点， $∠ ACD = ∠ B$ ．

（1）求证： $DC$ 为 $⊙ O$ 的切线；

（2）线段 $DF$ 分别交 $AC$ ， $BC$ 于点 $E$ ， $F$ 且 $∠ CEF = 45 °$ ， $⊙ O$ 的半径为5， $\sin B = \frac{3}{5}$ ，求 $CF$ 的长．

如图，在 $ΔABC$ 中，过点 $C$ 作 $CD / / AB$ ， $E$ 是 $AC$ 的中点，连接 $DE$ 并延长，交 $AB$ 于点 $F$ ，交 $CB$ 的延长线于点 $G$ ，连接 $AD$ ， $CF$ ．

（1）求证：四边形 $AFCD$ 是平行四边形．

（2）若 $GB = 3$ ， $BC = 6$ ， $BF = \frac{3}{2}$ ，求 $AB$ 的长．

如图，在平面直角坐标系中，一次函数 $y_{1} = ax + b$ 的图象与反比例函数 $y_{2} = \frac{k}{x}$ 的图象交于点 $A (1, 2)$ 和 $B (- 2, m)$ ．

（1）求一次函数和反比例函数的表达式；

（2）请直接写出 $y_{1} > y_{2}$ 时， $x$ 的取值范围；

（3）过点 $B$ 作 $BE / / x$ 轴， $AD ⊥ BE$ 于点 $D$ ，点 $C$ 是直线 $BE$ 上一点，若 $AC = 2 CD$ ，求点 $C$ 的坐标．

某商家销售一款商品，进价每件80元，售价每件145元，每天销售40件，每销售一件需支付给商场管理费5元，未来一个月（按30天计算），这款商品将开展“每天降价1元”的促销活动，即从第一天开始每天的单价均比前一天降低1元，通过市场调查发现，该商品单价每降1元，每天销售量增加2件，设第 $x$ 天 $(1 ⩽ x ⩽ 30$ 且 $x$ 为整数）的销售量为 $y$ 件．

（1）直接写出 $y$ 与 $x$ 的函数关系式；

（2）设第 $x$ 天的利润为 $w$ 元，试求出 $w$ 与 $x$ 之间的函数关系式，并求出哪一天的利润最大？最大利润是多少元？

试卷网试题网古诗词网作文网范文网