(本小题满分12分).一对父子参加一个亲子摸奖游戏,其规则如下:父亲在装有红色、白色球各两个的甲袋子里随机取两个球,儿子在装有红色、白色、黑色球各一个的乙袋子里随机取一个球,父子俩取球相互独立,两人各摸球一次合在一起称为一次摸奖,他们取出的三个球的颜色情况与他们获得的积分对应如下表:
| 所取球的情况 |
三个球均为红色 |
三个球均不同色 |
恰有两球为红色 |
其他情况 |
| 所获得的积分 |
180 |
90 |
60 |
0 |
(Ⅰ)求一次摸奖中,所取的三个球中恰有两个是红球的概率;
(Ⅱ)设一次摸奖中,他们所获得的积分为X,求X的分布列及均值(数学期望)E(X);
(Ⅲ)按照以上规则重复摸奖三次,求至少有两次获得积分为60的概率.
(本题满分10分)设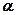 是第二象限的角,
是第二象限的角,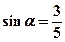 ,求
,求 的值.
的值.
(本小题满分15分)如图所示,已知椭圆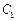 和抛物线
和抛物线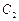 有公共焦点
有公共焦点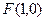 ,
, 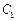 的中心和
的中心和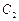 的顶点都在坐标原点,过点
的顶点都在坐标原点,过点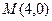 的直线
的直线 与抛物线
与抛物线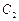 分别相交于
分别相交于 两点
两点
(1)写出抛物线
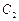 的标准方程;
的标准方程;
(2)若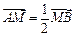 ,求直线
,求直线 的方程;
的方程;
(3)若坐标 原点
原点 关于直线
关于直线 的对称点
的对称点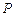 在抛物线
在抛物线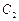 上,直线
上,直线 与椭圆
与椭圆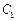 有公共点,求椭圆
有公共点,求椭圆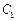 的长轴长的最小值。
的长轴长的最小值。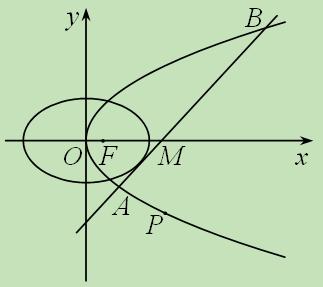
(本小题满分15分)
已知函数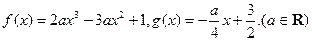
(I)当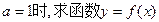 的单调区间;
的单调区间;
(II)若任意给定的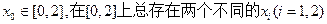 ,使得
,使得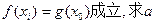 的取值范围。
的取值范围。
(本小题满分1 4分)右图为一简单组合体,其底面
4分)右图为一简单组合体,其底面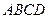 为正方形,
为正方形,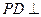 平面
平面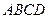 ,
,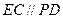 ,
,
且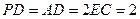
(1)求证: 平面
平面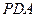
(2)求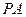 与平面
与平面 所成角的
所成角的 大小。
大小。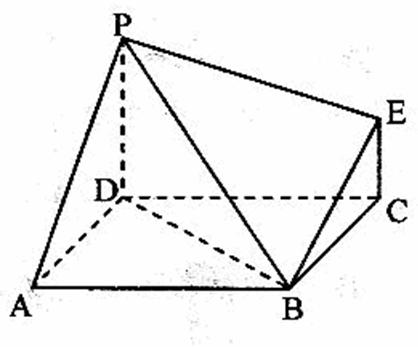
已知等差数列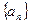
 满足前2项的和为5,前6项的和为3.
满足前2项的和为5,前6项的和为3.
(1)求数列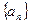 的通项公式;
的通项公式;
(2)设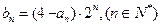 ,求数列
,求数列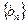 的前
的前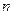 项和
项和