某校研究性学习小组从汽车市场上随机抽取 辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于
辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于 公里和
公里和 公里之间,将统计结果分
公里之间,将统计结果分
成 组:
组: ,
, ,
, ,
, ,
, ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
(1)求直方图中 的值;
的值;
(2)求续驶里程在 的车辆数;
的车辆数;
(3)若从续驶里程在 的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程为
的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程为 的概率.
的概率.
如图,在三棱柱 中,
中, 平面
平面 ,
, .以
.以 ,
, 为邻边作平行
为邻边作平行
四边形 ,连接
,连接 和
和 .
.
(1)求证:
 平面
平面 ;
;
(2)求证: 平面
平面 .
.
已知函数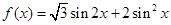 .
.
(1)求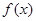 的最小正周期;
的最小正周期;
(2)求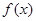 在区间
在区间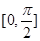 上的最大值和最小值.
上的最大值和最小值.
在数列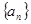 中,若
中,若 (
( ,
, ,
,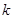 为常数),则称
为常数),则称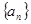 为
为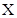 数列.
数列.
(1)若数列 是
是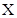 数列,
数列, ,
, ,写出所有满足条件的数列
,写出所有满足条件的数列 的前
的前 项;
项;
(2)证明:一个等比数列为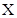 数列的充要条件是公比为
数列的充要条件是公比为 或
或 ;
;
(3)若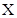 数列
数列 满足
满足 ,
,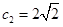 ,
,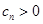 ,设数列
,设数列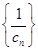 的前
的前 项和为
项和为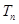 .是否存在
.是否存在
正整数
 ,使不等式
,使不等式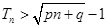 对一切
对一切 都成立?若存在,求出
都成立?若存在,求出
 的值;
的值;
若不存在,说明理由.
已知椭圆 :
: 的右焦点为
的右焦点为 ,短轴的一个端点
,短轴的一个端点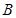 到
到 的距离等于焦距.
的距离等于焦距.
(1)求椭圆 的方程;
的方程;
(2)过点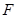 的直线
的直线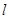 与椭圆
与椭圆 交于不同的两点
交于不同的两点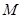 ,
,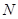 ,是否存在直线
,是否存在直线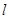 ,使得△
,使得△ 与△
与△ 的面积比值为
的面积比值为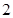 ?若存在,求出直线
?若存在,求出直线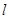 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.