(本小题满分12分)已知直线 的参数方程为
的参数方程为 (t为参数),以坐标原点为极点,
(t为参数),以坐标原点为极点, 正半轴为极轴,建立极坐标系,曲线
正半轴为极轴,建立极坐标系,曲线 的极坐标方程是
的极坐标方程是 .
.
(1)写出直线 的极坐标方程与曲线
的极坐标方程与曲线 的直角坐标方程;
的直角坐标方程;
(2)若点 是曲线
是曲线 上的动点,求
上的动点,求 到直线
到直线 距离的最小值,并求出此时
距离的最小值,并求出此时 点坐标.
点坐标.
数列 的前
的前 项和
项和 满足
满足 ,求
,求
数列 中,
中,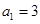 ,
,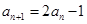 ,求
,求
求数列 的前
的前 项和
项和
设函数f(x)=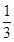 x3-ax(a>0),g(x)=bx2+2b﹣1.
x3-ax(a>0),g(x)=bx2+2b﹣1.
(1)若曲线y=f(x)与y=g(x)在它们的交点(1,c)处有相同的切线,求实数a,b的值;
(2)当b=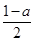 时,若函数h(x)=f(x)+g(x)在区间(﹣2,0)内恰有两个零点,求实数a的取值范围;
时,若函数h(x)=f(x)+g(x)在区间(﹣2,0)内恰有两个零点,求实数a的取值范围;
(3)当a=1,b=0时,求函数h(x)=f(x)+g(x)在区间[t,t+3]上的最小值.
已知椭圆(a>b>0)和直线l:y=bx+2,椭圆的离心率e= ,坐标原点到直线l的距离为
,坐标原点到直线l的距离为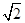 .
.
(1)求椭圆的方程;
(2)已知定点E(﹣1,0),若直线y=kx+2(k≠0)与椭圆相交于C,D两点,试判断是否存在实数k,使得以CD为直径的圆过定点E?若存在,求出k的值;若不存在,请说明理由.