某油厂从东北调运来的25吨大豆抵达火车站,营业部的王先生准备租用大小两种货车一次性把货物全部运走.已知1辆小货车和2辆大货车一次可以运货10.5吨;2辆小货车和1辆大货车一次可以运货9吨.问:王先生应租大、小两种货车各多少辆才能正好把货物一次全部运走?
四边形ABCD、DEFG都是正方形,连接AE、CG.
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
先化简,再求值: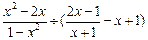 ,其中
,其中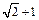 .
.
如图10-1,已知抛物线y = 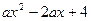 与x轴交于A、B两点,与y轴交于
与x轴交于A、B两点,与y轴交于
点C,且OB=OC.
(1)求抛物线的函数表达式;
(2)若点P是线段AB上的一个动点(不与A、B重合),分别以AP、BP为一边,在直线AB的同侧作等边三角形APM和BPN,求△PMN的最大面积,并写出此时点P的坐标;
(3)如图10-2,若抛物线的对称轴与x轴交于点D,F是抛物线上位于对称轴右侧的一个动点,直线FD与y轴交于点E.是否存在点F,使△DOE与△AOC相似?若存在,请求出点F的坐标;若不存在,请说明理由.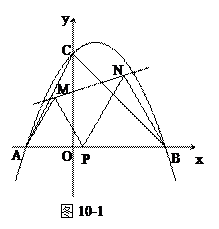

如图9-1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长 线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE = x,PC = y.
线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE = x,PC = y.
(1)求y与x之间的函数关系式;
(2)若PD是⊙O的切线,求x的值.
(3)过点D作DF⊥AE,垂足为H,交⊙O于点F,直线AF交BC于点G(如图9-2).若x=2,则sin∠BAG的值是_________.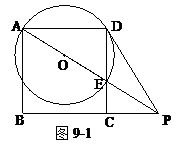
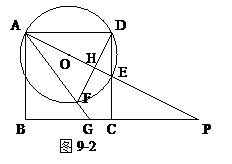
某校组织九年级师生共270人参观市文博会,若单独租用甲种客车,则刚好坐满;若单独租用乙种客车,则可以少租一辆,且余30个空座位.已知每辆乙种客车比甲种客车多15个座位.
(1)求甲、乙两种客车每辆的座位分别有多少个;
(2)该校决定这次参观活动同时租用这两种车,其中乙种客车比甲种客车多租1辆,这样要比单独租用一种车辆节省租金.已知甲种客车的租金为每辆250元,乙种客车的租金为每辆300元,请你帮助计算本次参观活动所需车辆的租金.