已知椭圆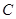 :
: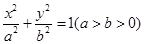 上的点到左焦点的最大距离是
上的点到左焦点的最大距离是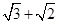 ,且点
,且点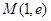 在椭圆
在椭圆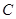 上,其中
上,其中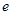 为椭圆
为椭圆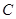 的离心率.
的离心率.
(Ⅰ)求椭圆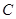 的方程;
的方程;
(Ⅱ)如图所示,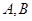 是椭圆
是椭圆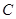 上的两点,且
上的两点,且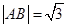 ,求
,求 面积的取值范围.
面积的取值范围.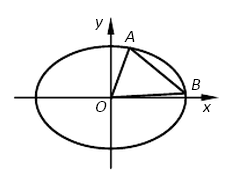
(本小题共13分)已知△ 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 ,
, .
.
(Ⅰ)若 ,求
,求 ;
;
(Ⅱ)若 ,求△
,求△ 的面积.
的面积.
已知函数f (x)=lnx,g(x)=ex.
(I)若函数φ (x) =" f" (x)- ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间;
(Ⅱ)设直线l为函数 y=f (x) 的图象上一点A(x0,f (x0))处的切线.证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
注:e为自然对数的底数.
已知焦点在 轴上的椭圆
轴上的椭圆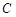 过点
过点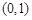 ,且离心率为
,且离心率为 ,
,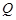 为椭圆
为椭圆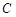 的左顶点.
的左顶点.
(Ⅰ)求椭圆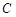 的标准方程;
的标准方程;
(Ⅱ)已知过点 的直线
的直线 与椭圆
与椭圆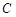 交于
交于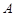 ,
,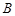 两点.
两点.
(ⅰ)若直线 垂直于
垂直于 轴,求
轴,求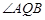 的大小;
的大小;
(ⅱ)若直线 与
与 轴不垂直,是否存在直线
轴不垂直,是否存在直线 使得
使得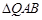 为等腰三角形?如果存在,求出直线
为等腰三角形?如果存在,求出直线 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
函数 的定义域为R,数列
的定义域为R,数列 满足
满足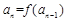 (
(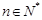 且
且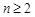 ).
).
(Ⅰ)若数列 是等差数列,
是等差数列, ,且
,且 (k为非零常数,
(k为非零常数, 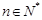 且
且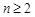 ),求k的值;
),求k的值;
(Ⅱ)若 ,
, ,
, ,数列
,数列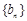 的前n项和为
的前n项和为 ,对于给定的正整数
,对于给定的正整数 ,如果
,如果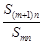 的值与n无关,求k的值.
的值与n无关,求k的值.
如图(1)在等腰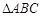 中,D,E,F分别是AB,AC和BC边的中点,
中,D,E,F分别是AB,AC和BC边的中点, ,现将
,现将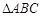 沿CD翻折成直二面角A-DC-B.(如图(2))
沿CD翻折成直二面角A-DC-B.(如图(2))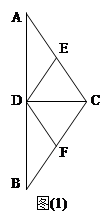

(I)试判断直线AB与平面DEF的位置关系,并说明理由;
(II)求二面角E-DF-C的余弦值;
(III)在线段BC是否存在一点P,但AP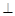 DE?证明你的结论.
DE?证明你的结论.