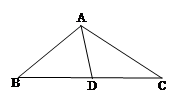(本小题满分12分)已知定义在 上的三个函数
上的三个函数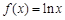 ,
, ,
, ,且
,且 在
在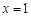 处取得极值.
处取得极值.


(Ⅰ)求 的值及函数
的值及函数 的单调区间.
的单调区间.
(Ⅱ)求证:当 时,恒有
时,恒有 成立.
成立.
(本小题满分12分)
已知函数
(1)求 的单调区间;
的单调区间;
(2)设 ,若对任意
,若对任意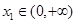 ,均存在
,均存在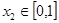 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知 F1、F2是椭圆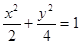 的两焦点,
的两焦点, 是椭圆在第一象限弧上一点,且满足
是椭圆在第一象限弧上一点,且满足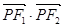 =1.过点P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
=1.过点P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
(1)求P点坐标;
(2)求证直线AB的斜率为定值;
(3)求△PAB面积的最大值.
(本小题满分12分)
从某校高三年级900名学生中随机抽取了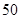 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于 和
和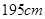 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组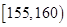 ,第二组
,第二组 …第八组
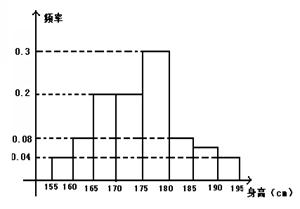
…第八组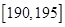 ,右图是按上述分组方法得到的条形图.
,右图是按上述分组方法得到的条形图.
(1)根据已知条件填写下面表格:
| 组 别 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 样本数 |
(2)估计这所学校高三年级900名学生中,身高在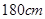 以上(含
以上(含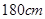 )的人数;
)的人数;
(3)在样本中,若第二组有 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有 人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,用
人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,用 表示实验小组中男同学的人数,求
表示实验小组中男同学的人数,求 的分布列及期望
的分布列及期望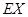
.
(本小题满分12分)
如图,在底面为直角梯形的四棱锥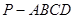 中,
中,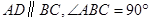 ,
,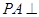 平面
平面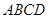 ,
, ,
,
(1) 求证: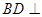 平面
平面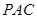 ;
;
(2) 求二面角 的大小.
的大小. 
(本小题满分12分)
如图,在△ABC中,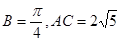 ,
,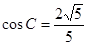 .
.
(1) 求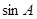 ;
;
(2) 设 的中点为
的中点为 ,求中线
,求中线 的长.
的长.