(本小题满分13分)已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元。设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为R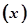 万元,且R
万元,且R
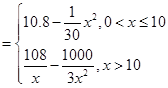
(1)写出年利润 (万元)关于年产量
(万元)关于年产量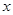 (千元)的函数解析式;
(千元)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大。(注:年利润=年销售收入-年总成本)
某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为 第二、第三门课程取得优秀成绩的概率分别为
第二、第三门课程取得优秀成绩的概率分别为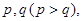 且不同课程是否取得优秀成绩相互独立,记
且不同课程是否取得优秀成绩相互独立,记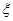 为该生取得优秀成绩的课程数,其分布列为
为该生取得优秀成绩的课程数,其分布列为
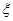 |
0 |
1 |
2 |
3 |
 |
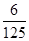 |
 |
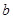 |
 |
(1)求该生至少有1门课程取得优秀成绩的概率;
(2)求 ,
,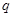 的值;
的值;
(3)求数学期望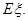
已知四棱锥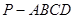 的底面
的底面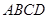 是边长为
是边长为 的正方形,
的正方形,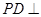 底面
底面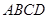 ,
,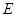 、
、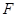 分别为棱
分别为棱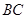 、
、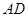 的中点.
的中点.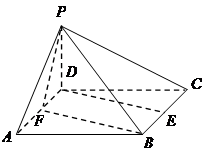
(1)求证: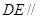 平面
平面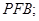
(2)已知二面角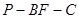 的余弦值为
的余弦值为 求四棱锥
求四棱锥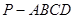 的体积.
的体积.
已知:以点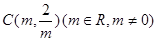 为圆心的圆与
为圆心的圆与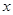 轴交于点
轴交于点 、
、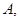 与
与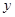 轴交于点
轴交于点 、
、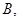 其中
其中 为原点.
为原点.
(1)求证: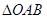 的面积为定值;
的面积为定值;
(2)设直线 与圆
与圆 交于点
交于点 、
、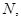 若
若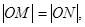 求⊙
求⊙ 的方程.
的方程.
在锐角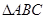 中,角
中,角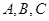 的对边分别为
的对边分别为 且
且 .
.
⑴求 的值;
的值;
⑵求 的取值范围.
的取值范围.
已知椭圆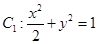 ,抛物线
,抛物线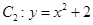 ,点
,点 是
是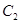 上的动点,过点
上的动点,过点 作抛物线
作抛物线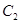 的切线
的切线 ,交椭圆
,交椭圆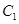 于
于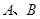 两点,
两点,
(1)当 的斜率是
的斜率是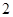 时,求
时,求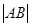 ;
;
(2)设抛物线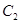 的切线方程为
的切线方程为 ,当
,当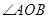 是锐角时,求
是锐角时,求 的取值范围.
的取值范围.