如图，已知椭圆
与
的中心在坐标原点
，长轴均为
且在
轴上，短轴长分别为
，
，过原点且不与轴重合的直线
与，的四个交点按纵坐标从大到小依次为
、
、
、
．记
，
和
的面积分别为
和
．
（1）当直线与
轴重合时，若
，求
的值；；
（2）设直线
，若
，证明：
是线段
的四等分点
（3）当变化时，是否存在与坐标轴不重合的直线，使得?并说明理由．
（本小题满分12分）已知函数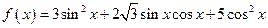
．
（Ⅰ）求函数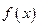
的周期和最大值；（Ⅱ）已知
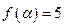，求
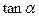的值．
（本小题满分14分）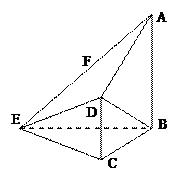
如图，在四棱锥E－ABCD中，AB⊥平面BCE，CD⊥平面BCE，
AB=BC=CE=2CD=2，∠BCE=1200，F为AE中点。
(Ⅰ) 求证：平面ADE⊥平面ABE ；
(Ⅱ)求二面角A—EB—D的大小的余弦值；
（Ⅲ）求点F到平面BDE的距离。
（本小题满分14分）已知数列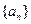
的首项
，
，
．
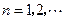（Ⅰ）求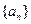的通项公式；（Ⅱ）证明：对任意的
，
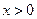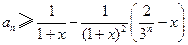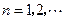，；（Ⅲ）证明：
．
（本小题满分14分）如图，已知直线l：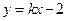
与抛物线C：
交于A，B两点，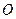
为坐标原点，
。
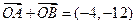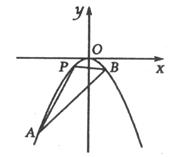
（Ⅰ）求直线l和抛物线C的方程；（Ⅱ）抛物线上一动点P从A到B运动时，求△ABP面积最大值．
（本小题满分12分）已知关于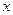
的一元二次函数
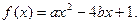（Ⅰ）设集合P={1，2， 3}和Q={－1，1，2，3，4}，分别从集合P和Q中随机取一个数作为
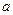和
，求函数
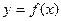在区间[
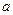上是增函数的概率；（Ⅱ）设点（，）是区域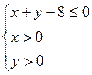
内的随机点，求函数
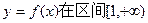上是增函数的概率。