已知某市的光明中学、市图书馆和光明电影院在同一直线上,它们之间的距离如图所示.小张星期天上午带了75元现金先从光明中学乘出租车去了市图书馆,付费9元;中午再从市图书馆乘出租车去了光明电影院,付费12.6元.若该市出租车的收费标准是:不超过3公里计费为m元,3公里后按n元/公里计费.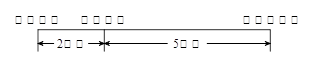
(1)求m,n的值,并直接写出车费y(元)与路程x(公里)(x>3)之间的函数关系式;
(2)如果小张这天外出的消费还包括:中午吃饭花费15元,在光明电影院看电影花费25元.问小张剩下的现金够不够乘出租车从光明电影院返回光明中学?为什么?
已知椭圆的一个顶点为A(0,-1),焦点在x轴上,若右焦点到直线 的距离为3。
的距离为3。
(1)求椭圆的方程;
(2)设直线 与椭圆相交于不同的两点M,N,当|AM|=|AN|时,求m的取值范围.
与椭圆相交于不同的两点M,N,当|AM|=|AN|时,求m的取值范围.
已知函数
(1)若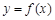 的图象在点
的图象在点 处的切线方程为
处的切线方程为 ,求
,求 在区间
在区间 上的最大值;
上的最大值;
(2)当 时,若
时,若 在区间
在区间 上不单调,求
上不单调,求 的取值范围.
的取值范围.
如图,在三棱锥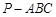 中,
中, 平面
平面 ,
,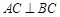 ,
, 为侧棱
为侧棱 上一点,它的正(主)视图和侧(左)视图如图所示.
上一点,它的正(主)视图和侧(左)视图如图所示.
(1)证明: 平面
平面 ;
;
(2)求三棱锥 的体积;
的体积;
(3)在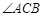 的平分线上确定一点
的平分线上确定一点 ,使得
,使得 平面
平面 ,并求此时
,并求此时 的长.
的长.
某班级共有60名学生,先用抽签法从中抽取部分学生调查他们的学习情况,若每位学生被抽到的概率为.
(1)求从中抽取的学生数;
(2)若抽查结果如下,先确定x,再完成频率分布直方图;
| 每周学习时间(小时) |
[0,10) |
[10,20) |
[20,30) |
[30,40 |
| 人数 |
2 |
4 |
x |
1 |
(3)估计该班学生每周学习时间的平均数(同一组中的数据用该组区间的中点值作代表).
已知函数f(x)= (其中A>0,
(其中A>0,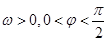 )的图象如图所示。
)的图象如图所示。
(1)求A,w及j的值;
(2)若tana=2,求 的值.
的值.