某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
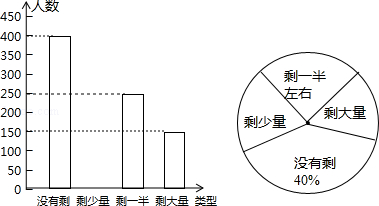
(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐?
给定椭圆C: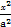 +
+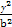 =1(a>b>0),称圆心在原点O,半径为
=1(a>b>0),称圆心在原点O,半径为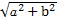 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(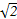 ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为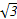 .
.
(1)求椭圆C的方程和其“准圆”的方程.
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线l1,l2使得l1,l2与椭圆C都只有一个交点,且l1,l2分别交其“准圆”于点M,N.
①当P为“准圆”与y轴正半轴的交点时,求l1,l2的方程;
②求证:|MN|为定值.
已知椭圆E: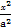 +
+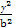 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=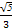 ,a2与b2的等差中项为
,a2与b2的等差中项为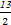 .
.
(1)求椭圆E的方程.
(2)A,B是椭圆E上的两点,线段AB的垂直平分线与x轴相交于点P(t,0),求实数t的取值范围.
如图,已知椭圆C: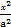 +y2=1(a>1)的上顶点为A,离心率为
+y2=1(a>1)的上顶点为A,离心率为 ,若不过点A的动直线l与椭圆C相交于P,Q两点,且
,若不过点A的动直线l与椭圆C相交于P,Q两点,且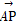 ·
·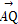 =0.
=0.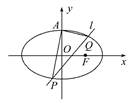
(1)求椭圆C的方程.
(2)求证:直线l过定点,并求出该定点N的坐标.
已知中心在原点的椭圆C的一个焦点为F(4,0),长轴端点到较近焦点的距离为1,A(x1,y1),B(x2,y2)(x1≠x2)为椭圆上不同的两点.
(1)求椭圆C的方程.
(2)若x1+x2=8,在x轴上是否存在一点D,使|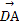 |=|
|=|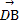 |?若存在,求出D点的坐标;若不存在,说明理由.
|?若存在,求出D点的坐标;若不存在,说明理由.
已知平面内一动点P到点F(1,0)的距离与点P到y轴的距离的差等于1.
(1)求动点P的轨迹C的方程.
(2)过点F作两条斜率存在且互相垂直的直线l1,l2,设l1与轨迹C相交于点A,B,l2与轨迹C相交于点D,E,求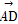 ·
·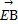 的最小值.
的最小值.