给定数列 ,如果存在常数
,如果存在常数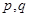 使得
使得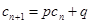 对任意
对任意 都成立,则称
都成立,则称 为“M类数列”
为“M类数列”
(1)若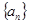 是公差为
是公差为 的等差数列,判断
的等差数列,判断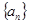 是否为“M类数列”,并说明理由;
是否为“M类数列”,并说明理由;
(1)若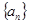 是“M类数列”且满足:
是“M类数列”且满足: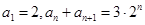
①求 及
及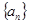 的通项公式;
的通项公式;
②设数列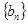 满足:对任意的正整数
满足:对任意的正整数 ,都有
,都有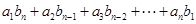
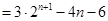 ,且集合
,且集合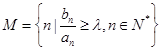 中有且仅有3个元素,试求实数
中有且仅有3个元素,试求实数 的取值范围.
的取值范围.
(本小题 满分12分)
满分12分)
已知等差数列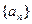 满足
满足
(1)求数列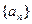 的通项公式;
的通项公式;
(2)设各项均为正数的等比数列 的前n项和为Tn若
的前n项和为Tn若 求
求
(本小题满分14分)
设数列 的通项公式为
的通项公式为 . 数列
. 数列 定义如下:对于正整数m,
定义如下:对于正整数m,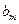 是使得不等式
是使得不等式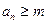 成立的所有n中的最小值.
成立的所有n中的最小值.
(Ⅰ)若 ,求
,求 ;
;
(Ⅱ)若 ,求数列
,求数列 的前2m项和公式;
的前2m项和公式;
(Ⅲ)是否存在p和q,使得 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.
(本小题满分14分)
已知圆 方程为:
方程为: .
.
(Ⅰ)直线 过点
过点 ,且与圆
,且与圆 交于
交于 、
、 两点,若
两点,若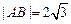 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)过圆 上一动点
上一动点 作平行于
作平行于 轴的直线
轴的直线 ,设
,设 与
与 轴的交点为
轴的交点为 ,若向量
,若向量 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
(本小题满分14分)
如图,在四棱锥 中,
中, ,
,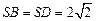 ,底面
,底面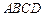 是菱形,且
是菱形,且 ,
,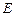 为
为 的中点.
的中点.
(Ⅰ)证明: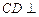 平面
平面 ;
;
(Ⅱ)侧棱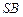 上是否存在点
上是否存在点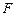 ,使得
,使得 平面
平面 ?并证明你的结论.
?并证明你的结论.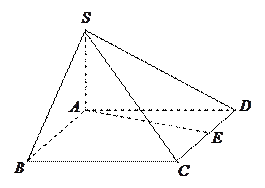
(本小题满分14分)
设某旅游景点每天的固定成本为500元,门票每张为30元,变动成本与购票进入旅游景点的人数的算术平方根成正比。一天购票人数为25时,该旅游景点收支平衡;一天购票人数超过100时,该旅游景点须另交保险费200元。设每天的购票人数为 ,盈利额为
,盈利额为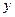 元。
元。
(Ⅰ)求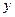 与
与 之间的函数关系;
之间的函数关系;
(Ⅱ)该旅游景点希望在人数达到20人时即不出现亏损,若用提高门票价格的措施,则每张门票至少要多少元(取整数)?
(参考数据: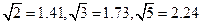 .)
.)