(本小题满分12分)如图,茎叶图记录了甲组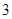 名同学寒假假期中去
名同学寒假假期中去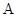 图书馆学习的次数和乙组
图书馆学习的次数和乙组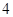 名同学寒假假期中去
名同学寒假假期中去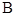 图书馆学习的次数,乙组记录中有一个数据模糊,无法确认,在图中以
图书馆学习的次数,乙组记录中有一个数据模糊,无法确认,在图中以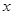 表示.
表示.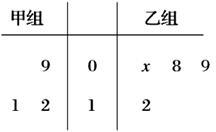
(1)如果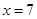 ,求乙组同学去图书馆学习次数的平均数和方差;
,求乙组同学去图书馆学习次数的平均数和方差;
(2)如果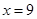 ,从学习次数大于
,从学习次数大于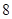 的学生中等可能地选
的学生中等可能地选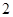 名同学,求选出的
名同学,求选出的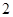 名同学恰好分别在两个图书馆学习且学习的次数和大于
名同学恰好分别在两个图书馆学习且学习的次数和大于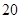 的概率.
的概率.
(本小题满分12分)已知函数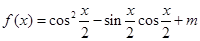 ,当
,当 时,函数
时,函数 的最大值为
的最大值为 .
.
(1)求函数 的值;
的值;
(2)若 ,求
,求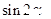 的值.
的值.
(本小题满分14分)已知函数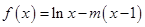 (
(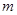 为常数且
为常数且 ).
).
(1)求函数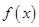 的单调区间.
的单调区间.
(2)若函数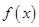 在点
在点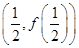 处的切线与直线
处的切线与直线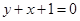 相互垂直.
相互垂直.
①求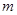 的值;
的值;
②在①的条件下,证明:对于任意的 ,都有
,都有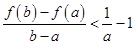 成立.
成立.
(本小题满分14分)已知函数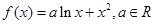
(Ⅰ)若函数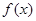 在
在 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;
(Ⅱ)当 时,求函数
时,求函数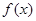 在[1,e]上的最小值及相应的x值;
在[1,e]上的最小值及相应的x值;
(Ⅲ)若存在 [1,e],使得
[1,e],使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)如图,圆 的方程为
的方程为 ,
, 是圆
是圆 外一个定点,
外一个定点, 是线段
是线段 的中点,
的中点,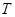 是圆上任意一点,线段
是圆上任意一点,线段 的垂直平分线
的垂直平分线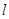 和半径
和半径 所在直线相交于点
所在直线相交于点 .
.
(Ⅰ)当点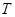 在圆上运动时,求证:点
在圆上运动时,求证:点 的轨迹
的轨迹 为双曲线,并求轨迹
为双曲线,并求轨迹 的方程;
的方程;
(Ⅱ)若 是双曲线
是双曲线 的左顶点,设过双曲线
的左顶点,设过双曲线 右焦点
右焦点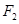 的直线
的直线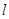 与双曲线
与双曲线 的右支交于
的右支交于 两点,其中点位于第一象限内.若直线
两点,其中点位于第一象限内.若直线 分别与直线
分别与直线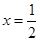 交于
交于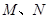 两点,求证:
两点,求证: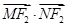 为定值;
为定值;
(本小题满分12分)为了统计福州某地区网友2014年12月12日在某淘宝店的网购情况,随机抽查了该地区 名网友当天的网购金额情况,得到如下数据统计表(如图1):
名网友当天的网购金额情况,得到如下数据统计表(如图1):
若网购金额超过 千元的顾客定义为“网购达人”,网购金额不超过
千元的顾客定义为“网购达人”,网购金额不超过 千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为
千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为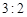 .
.
(Ⅰ)试确定 ,
,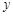 ,
, ,
,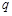 的值,并补全频率分布直方图(如图2).
的值,并补全频率分布直方图(如图2).
(Ⅱ)为了进一步了解这 名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定
名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定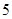 人,若需从这
人,若需从这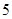 人中随机选取
人中随机选取 人进行问卷调查.求进行问卷调查人中至少有2人是“非网购达人”的概率.
人进行问卷调查.求进行问卷调查人中至少有2人是“非网购达人”的概率.