某渔业公司今年初用98万元购进一艘渔船用于捕捞,第一年需各种费用12万元,从第二年开始包括维修费在内,每年所需费用均比上一年增加4万元,该船每年捕捞的总收入为50万元.
(1)该船捕捞几年开始盈利?(即总收入减去成本及所有费用之差为正值)
(2)该船捕捞若干年后,处理方案有两种:
①当年平均盈利达到最大值时,以26万元的价格卖出;
②当盈利总额达到最大值时,以8万元的价格卖出.问哪一种方案较为合算,请说明理由.
《选修4-5:不等式选讲》已知函数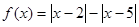 .
.
(1)证明: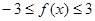 ;
;
(2)求不等式 的解集.
的解集.
《选修4-4:坐标系与参数方程》已知直线L的参数方程: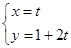 (t为参数)和圆C的极坐标方程:
(t为参数)和圆C的极坐标方程: 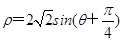 (θ为参数).
(θ为参数).
(1)求圆C的直角坐标方程.
(2)判断直线L和圆C的位置关系.
已知函数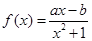 在点
在点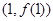 的切线方程为
的切线方程为 .
.
(1)求函数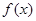 的解析式;
的解析式;
(2)设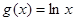 ,求证:
,求证: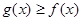 在
在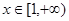 上恒成立.
上恒成立.
已知椭圆C的中心在原点,焦点在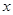 轴上,左右焦点分别为
轴上,左右焦点分别为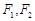 ,且
,且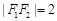 ,点(1,
,点(1,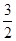 )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的方程;
(2)过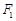 的直线
的直线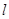 与椭圆
与椭圆 相交于
相交于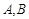 两点,且
两点,且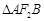 的面积为
的面积为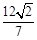 ,求直线
,求直线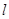 的方程.
的方程.
为迎接高一新生报到,学校向高三甲、乙、丙、丁四个实验班征召志愿者.统计如下:
| 班级 |
甲 |
乙 |
丙 |
丁 |
| 志愿者人数 |
45 |
60 |
30 |
15 |
为了更进一步了解志愿者的来源,采用分层抽样的方法从上述四个班的志愿者中随机抽取50名参加问卷调查.
(1)从参加问卷调查的50名志愿者中随机抽取两名,求这两名来自同一个班级的概率;
(2)在参加问卷调查的50名志愿者中,从来自甲、丙两个班级的志愿者中随机抽取两名,用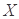 表示抽得甲班志愿者的人数,求
表示抽得甲班志愿者的人数,求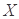 的分布列和数学期望.
的分布列和数学期望.