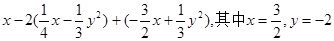在正方形ABCD中,点M是射线BC上一点,点N是CD的延长线上一点,且BM=DN,直线BD与MN相交于点E.
(1)如图1,当点M在线段BC上时,求证:BD-2DE=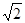 BM;
BM;
(2)如图2,当点M在BC的延长线上时,BD、DE、BM之间满足的关系式是____;
(3)在⑵的条件下,连接BN交AD于F,连接MF交BD于G,若DE=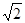 ,且AF:FD=1:2,求线段DG的长.
,且AF:FD=1:2,求线段DG的长.
(本题7分)如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
| 9 |
a |
b |
c |
-5 |
1 |
… |
(1)可求得c=_______,第2006个格子中的数为___________;
(2)如果x、y为前三个格子中的任意两个数,那么所有的∣x-y∣的和可以通过计算
∣9-a∣+∣a-9∣+∣9-b∣+∣b-9∣+∣a-b∣+∣b-a∣得到,求所有的∣x-y∣的和;
(3)前m个格子中所填整数之和是否可能为2014?若能,求m的值;若不能,请说出理由.
(本题8分) 某单位在二月份准备组织部分员工到北京旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为2000元/人,两家旅行社同时都对10人以上的团体推出了优惠举措:甲旅行社对每位员工七五折优惠;而乙旅行社是免去一位带队管理员工的费用,其余员工八折优惠.
(1)如果设参加旅游的员工共有a(a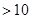 )人,则甲旅行社的费用为元,乙旅行社的费用为元;(用含a的代数式表示,并化简.)
)人,则甲旅行社的费用为元,乙旅行社的费用为元;(用含a的代数式表示,并化简.)
(2)假如这个单位现组织包括管理员工在内的共20名员工到北京旅游,该单位选择哪一家旅行社比较优惠?请说明理由;
(3)如果计划在二月份外出旅游七天,设最中间一天的日期为m.
①这七天的日期之和为;(用含m的代数式表示,并化简.)
②假如这七天的日期之和为63的倍数,则他们可能于二月几号出发?(写出所有符合条件的可能性,并写出简单的计算过程.)
(本题6分) 有理数 <0 、
<0 、 >0 、
>0 、 >0,且
>0,且 ,
,
(1)在数轴上将a、b、c三个数填在相应的括号中.
(2)化简:
(本题8分)解方程:
(1) 2(x-2)=3(4x-1)+9(2) 
(本题5分)化简求值: