“水资源与永恒发展”是2015年联合国世界水资源日主题．近年来，某企业每年需要向自来水厂缴纳水费约4万元，为了缓解供水压力，决定安装一个可使用4年的自动污水净化设备，安装这种净水设备的成本费（单位：万元）与管线、主体装置的占地面积（单位：平方米）成正比，比例系数约为0．2．为了保证正常用水，安装后采用净水装置净水和自来水厂供水互补的用水模式．假设在此模式下，安装后该企业每年向自来水厂缴纳的水费 C（单位：万元）与安装的这种净水设备的占地面积x（单位：平方米）之间的函数关系是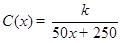
（x≥0，k为常数）．记y为该企业安装这种净水设备的费用与该企业4年共将消耗的水费之和．
（1）试解释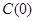
的实际意义，请建立y关于x的函数关系式并化简；
（2）当x为多少平方米时，y取得最小值？最小值是多少万元？
（本小题满分14分）
如图所示，已知曲线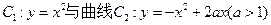
交于点O、A，直线
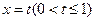与曲线
、
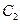分别交于点D、B，连结OD，DA，AB.
（1）求证:曲边四边形ABOD（阴影部分：OB为抛物线弧）的面积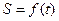
的函数表达式为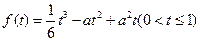
（2）求函数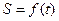在区间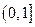
上的最大值.
（本小题满分13分）
甲、乙两人各射击一次，击中目标的概率分别是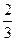
和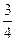
，假设两个射击是否击中目标，相互之间没有影响；每人各次射击是否中目标相互之间也没有影响。
（1）求甲射击4次，至少有1次未击中目标的概率；
（2）求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率；
（3）假设某人连续2次未击中目标，则中止其射击。则乙恰好射击5次后被中止射击的概率是多少？
（本小题满分13分）
设函数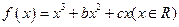
，已知
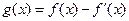是奇函数.
（Ⅰ）求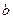
、
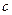的值;（Ⅱ）求
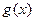的单调区间与极值.
（本小题满分13分）
已知
的展开式中第五项的系数与第三项的系数的比是10:1
（1）求展开式中各项系数的和；
（2）求展开式中含
的项；
（本小题满分13分）
4位学生与2位教师并坐合影留念，针对下列各种坐法，试问：各有多少种不同的坐法？（用数字做答）
（1）教师必须坐在中间；
（2）教师不能坐在两端，但要坐在一起；
（3）教师不能坐在两端，且不能相邻．