选修4-4 极坐标与参数方程
已知曲线 的极坐标方程为
的极坐标方程为 ,将曲线
,将曲线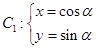 (
(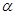 为参数)经过伸缩变换
为参数)经过伸缩变换 后得到曲线
后得到曲线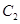 .
.
(1)求曲线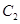 的参数方程;
的参数方程;
(2)若点 在曲线
在曲线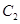 上运动,试求出
上运动,试求出 到曲线
到曲线 的距离的最小值.
的距离的最小值.
(16分)已知函数 (
(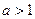 ).
).
(I)若 的定义域和值域均是
的定义域和值域均是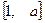 ,求实数
,求实数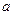 的值;
的值;
(II)若 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的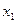 ,
,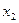
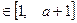 ,总有
,总有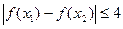 ,求实数
,求实数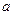 的取值范围.
的取值范围.
(14分)已知函数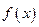 在定义域
在定义域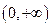 上为增函数,且满足
上为增函数,且满足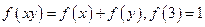
(1)求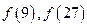 的值 (2)解不等式
的值 (2)解不等式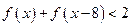
(14分) 已知等差数列的定义为:在一个数列中,从第二项起,如果每一项与它的前一项的差都为同一个常数,那么这个数列叫做等差数列,这个常数叫做该数列的公差.(1)类比等差数列的定义给出“等和数列”的定义;(2) 已知数列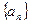 是等和数列,且
是等和数列,且 ,公和为
,公和为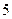 ,求
,求  的值,并猜出这个数列的通项公式(不要求证明)。
的值,并猜出这个数列的通项公式(不要求证明)。
(14分)已知集合A={x|x2-2x-8≤0,x∈R},B={x|x2-(2m-3)x+m2-3m≤0,x∈R,m∈R }.
(1)若A∩B=[2,4],求实数m的值;
(2)设全集为R,若A ∁RB,求实数m的取值范围.
∁RB,求实数m的取值范围.
(本小题满分12分)
已知点 、
、 、
、 的坐标分别为
的坐标分别为
 ,
, ,
, (
( ),其中
),其中 ,
,
(1)若 ,
, 的值;
的值;
(2)记 ,若
,若 的最大值为
的最大值为 ,求实数
,求实数 的值.
的值.