已知两个正数a,b满足a+b=1
(1)求证: ;
;
(2)若不等式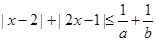 对任意正数a,b都成立,求实数x的取值范围.
对任意正数a,b都成立,求实数x的取值范围.
已知直线 :
: (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为 .
.
(1)将曲线C的极坐标方程化为直坐标方程;
(2)设点M的直角坐标为 ,直线l与曲线C的交点为A,B,求|MA|•|MB|的值.
,直线l与曲线C的交点为A,B,求|MA|•|MB|的值.
已知 二项展开式中,第4项的二项式系数与第3项的二项式系数的比为8:3
二项展开式中,第4项的二项式系数与第3项的二项式系数的比为8:3
(1)求n的值;
(2)求展开式中 项的系数
项的系数
(3)计算式子 的值.
的值.
如图,在平面直角坐标系中,抛物线y=ax2+bx-3与x轴交于点A(-1,0)、B (3,0)两点,直线y=x-2与x轴交于点D.与y轴交于点C.点P是x轴下方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式;
(2)若PE=3EF,求m的值.
如图,已知矩形OABC中,OA=3,AB=4,双曲线y= (k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD
(k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD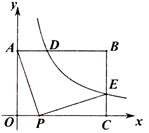
(1)求k的值和点E的坐标;
(2)点P是线段OC上的一个动点,是否存在点P,使∠APE=90°?若存在,求出此时点P的坐标,若不存在,请说明理由.