已知{ }是首项为
}是首项为 ,公差为
,公差为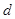 的等差数列,
的等差数列, 是其前
是其前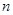 项的和,且
项的和,且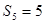 ,
, .
.
(Ⅰ)求数列{ }的通项
}的通项 及
及 ;
;
(Ⅱ)设 是首项为1,公比为3的等比数列.求数列{
是首项为1,公比为3的等比数列.求数列{ }的通项公式及其前
}的通项公式及其前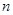 项和
项和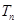
在 中,角 所对应的边为
(1)若
,求
的值;
(2)若
,求
的值.
在平面直角坐标系 上,给定抛物线 .实数 满足 , 是方程 的两根,记
(1)过点 作 的切线教 轴于点 .证明:对线段 上任一点 有 ;
(2)设 是定点,其中 满足 , .过 作 的两条切线 ,切点分别为 , 与y轴分别交与 .线段 上异于两端点的点集记为 .证明: ;
(3)设 .当点 取遍 时,求 的最小值(记为 )和最大值(记为 ).
设 ,数列 满足 , ,
(1)求数列 的通项公式.
(2)证明:对于一切正整数 ,
设圆 与两圆 中的一个内切,另一个外切.
(1)求 的圆心轨迹 的方程.
(2)已知点 , 且 为 上动点,求 的最大值及此时点 的坐标.
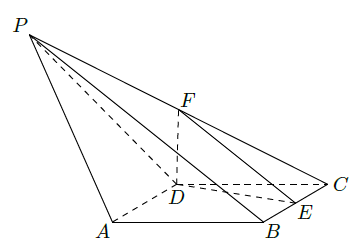
如图,在锥体 中,ABCD是边长为1的菱形,且 , , ,E,F分别是BC,PC的中点.
(1)证明:
(2)求二面角 的余弦值