如图，已知矩形ABCD是圆柱O1O2的轴截面，N在上底面的圆-优题课

题文

如图，已知矩形ABCD是圆柱O₁O₂的轴截面，N在上底面的圆周O₂上，AC、BD相交于点M；

（1）求证：CN⊥平面ADN；
（2）已知圆锥MO₁和圆锥MO₂的侧面展开图恰好拼成一个半径为2的圆，直线BC与平面CAN所成角的正切值为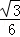，求异面直线AB与DN所成角的值．

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

设 ${a_{n}}$ 的公比不为1的等比数列，其前 $n$ 项和为 $S_{n}$ ，且 $a_{5}, a_{3}, a_{4}$ 成等差数列。
（1）求数列 ${a_{n}}$ 的公比；（2）证明：对任意 $k \in N_{+_{}}$ ， $S_{k + 2}, S_{k}, S_{k + 1}$ 成等差数列

函数 $f (x) = A \sin (ω x - \frac{π}{6}) + 1, (A > 0, ω > 0)$ 的最大值为3，其图像相邻两条对称轴之间的距离为 $\frac{π}{2}$ .
（1）求函数 $f (x)$ 的解析式；
（2）设 $α \in (0, \frac{π}{2})$ ，则 $f (\frac{α}{2}) = 2$ ，求 $α$ 的值

设 $A$ 是如下形式的2行3列的数表，

$a$	$b$	$c$
$d$	$e$	$f$

满足性质 $P : a, b, c, d, e, f$ $\in [- 1, 1]$ ，且 $a + b + c + d + e + f = 0$

记 $r_{i} (A)$ 为 $A$ 的第 $i$ 行各数之和（ $i$ =1,2）, $c_{j} (A)$ 为 $A$ 的第 $j$ 列各数之和（ $j$ =1,2,3）记 $k (A)$ 为 $|r_{1} (A), r_{2} (A), c_{1} (A), c_{2} (A), c_{3} (A)|$ 中的最小值。
（1）对如下表 $A$ ，求 $k (A)$ 的值

1	1	$- 0.8$
$0.1$	$- 0.3$	$- 1$

(2)设数表 $A$ 形如

1	1	- 1 - 2 d
$d$	$d$	- $1$

其中 $- 1 \leq d \leq 0$ ，求 $k (A)$ 的最大值
（3）对所有满足性质P的2行3列的数表 $A$ ，求 $k (A)$ 的最大值。

已知椭圆 $C$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的一个顶点为 $A$ （2,0），离心率为 $\frac{\sqrt{2}}{2}$ ，直线 $y = k (x - 1)$ 与椭圆 $C$ 交于不同的两点 $M, N$ 。
（1）求椭圆 $C$ 的方程
（2）当 $△ A M N$ 的面积为 $\frac{\sqrt{10}}{3}$ 时，求 $k$ 的值。

已知函数 $f (x) = a x^{2} + 1 (a > 0), g (x) = x^{3} + b x$ .

（1）若曲线 $y = f (x)$ 与曲线 $y = g (x)$ 在它们的交点 $(1, c)$ 处具有公共切线，求 $a, b$ 的值
（2）当 $a = 3, b = - 9$ 时，若函数 $f (x) + g (x)$ 在区间 $[k, 2]$ 上的最大值为28,求 $k$ 的取值范围

试卷网试题网古诗词网作文网范文网