在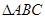 中,已知
中,已知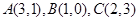 .
.
(1)判断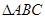 的形状;
的形状;
(2)设O为坐标原点,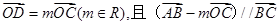 ,求
,求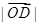 .
.
已知向量 ,
,  ,
, .
.
(1)若 ,求向量
,求向量 、
、 的夹角
的夹角 ;
;
(2)若 ,函数
,函数 的最大值为
的最大值为 ,求实数
,求实数 的值.
的值.
如图,用半径为 cm,面积为
cm,面积为 cm2的扇形铁皮制作一个无盖的圆锥形容器(衔接部分忽略不计), 该容器最多盛水多少?(结果精确到0.1 cm3)
cm2的扇形铁皮制作一个无盖的圆锥形容器(衔接部分忽略不计), 该容器最多盛水多少?(结果精确到0.1 cm3)
已知椭圆 的离心率为
的离心率为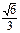 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为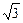 .
.
(1)求椭圆C的方程;
(2)设直线l与椭圆c交于A、B两点,坐标原点O到直线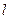 的距离为
的距离为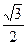 ,求
,求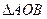 面积的最大值.
面积的最大值.
某商场经销某商品,根据以往资料统计,顾客采用的付款期数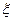 的分布列为
的分布列为
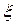 |
1 |
2 |
3 |
4 |
5 |
 |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分二期或3期付款,其利润为250元;分4期或5期付款,其利润为300元。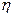 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求事件A:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率.
(2)求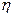 的分布列及期望.
的分布列及期望.
一个袋中有1个白球和4个黑球,每次从中任取一个球,每次所取的球放回,直到取得白球为止,但摸球次数不超过5次,求取球次数的分布列