已知向量
(1)当 时,求
时,求 的值;
的值;
(2)求 在
在 上的值域.
上的值域.
(本小题满分13分)
已知函数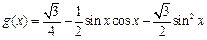 的图象按向量
的图象按向量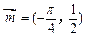 平移得到函数
平移得到函数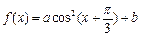 的图象.
的图象.
(1)求实数a、b的值;
(2)设函数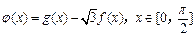 ,求函数
,求函数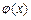 的单调递增区间和最值.
的单调递增区间和最值.
(本小题满分12分)
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有n( )个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.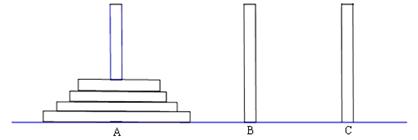
现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数,回答下列问题:
(1)写出a1,a2,a3,并求出an;
(2)记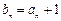 ,求和
,求和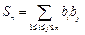 (
(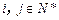 );
);
(其中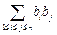 表示所有的积
表示所有的积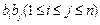 的和)
的和)
(3)证明: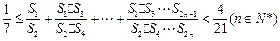 .
.
(本小题满分12分)
设F是椭圆C: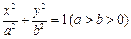 的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知
的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知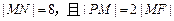 .
.
(1)求椭圆C的标准方程;
(2)若过点P的直线与椭圆相交于不同两点A、B求证:∠AFM =∠BFN;
(3)求三角形ABF面积的最大值.
(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是矩形,已知AB = 3,AD = 2,PA = 2,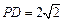 ,
,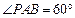 .
.
(1)证明:AD⊥平面PAB;
(2)求异面直线PC与AD所成的角的大小;
(3)求二面角P—BD—A的大小.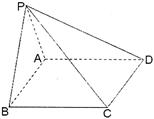
(本小题满分13分)
已知函数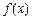 的导数
的导数 .a,b为实数,
.a,b为实数,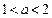 .
.
(1)若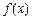 在区间
在区间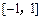 上的最小值、最大值分别为
上的最小值、最大值分别为 、1,求a、b的值;
、1,求a、b的值;
(2)在 (1) 的条件下,求曲线在点P(2,1)处的切线方程;
(3)设函数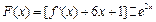 ,试判断函数
,试判断函数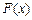 的极值点个数.
的极值点个数.