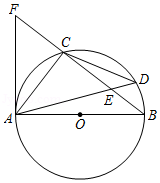
如图，在边长为1的正方形组成的方格中，点，都在格点上．（1）-优题课

如图，在边长为1的正方形组成的方格中，点，都在格点上．

（1）在给定的方格中将线段平移到，使得四边形是矩形，且点，都落在格点上．画出四边形，并叙述线段的平移过程；

（2）在方格中画出关于直线对称的；

（3）直接写出与的交点到线段的距离．

科目数学题型解答题难度中等

知识点：作图-平移变换作图-轴对称变换相似三角形的判定与性质矩形的性质

先化简，再求值： $(\frac{x - 1}{x + 1} + 1) \div \frac{x^{3} - 2 x^{2} + x}{x^{2} - 1}$ ，其中 $x = \sqrt{3} + 1$ ．

在平面直角坐标系中，抛物线 $y = a x^{2} + bx + 2 (a \neq 0)$ 经过点 $A (- 2, - 4)$ 和点 $C (2, 0)$ ，与 $y$ 轴交于点 $D$ ，与 $x$ 轴的另一交点为点 $B$ ．

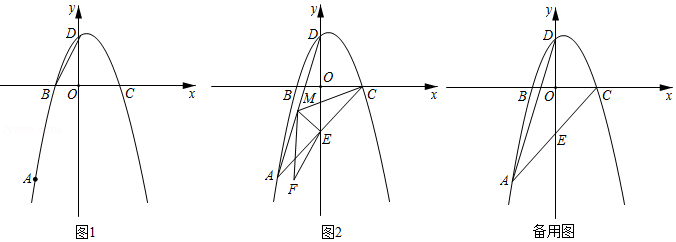
（1）求抛物线的解析式；

（2）如图1，连接 $BD$ ，在抛物线上是否存在点 $P$ ，使得 $∠ PBC = 2 ∠ BDO$ ？若存在，请求出点 $P$ 的坐标；若不存在，请说明理由；

（3）如图2，连接 $AC$ ，交 $y$ 轴于点 $E$ ，点 $M$ 是线段 $AD$ 上的动点（不与点 $A$ ，点 $D$ 重合），将 $ΔCME$ 沿 $ME$ 所在直线翻折，得到 $ΔFME$ ，当 $ΔFME$ 与 $ΔAME$ 重叠部分的面积是 $ΔAMC$ 面积的 $\frac{1}{4}$ 时，请直接写出线段 $AM$ 的长．

在矩形 $ABCD$ 中，点 $E$ 是射线 $BC$ 上一动点，连接 $AE$ ，过点 $B$ 作 $BF ⊥ AE$ 于点 $G$ ，交直线 $CD$ 于点 $F$ ．

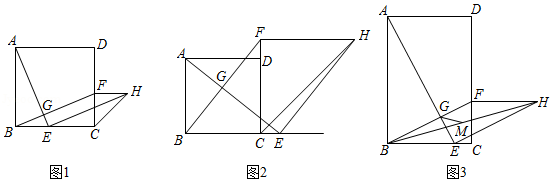
（1）当矩形 $ABCD$ 是正方形时，以点 $F$ 为直角顶点在正方形 $ABCD$ 的外部作等腰直角三角形 $CFH$ ，连接 $EH$ ．

①如图1，若点 $E$ 在线段 $BC$ 上，则线段 $AE$ 与 $EH$ 之间的数量关系是　　，位置关系是　　；

②如图2，若点 $E$ 在线段 $BC$ 的延长线上，①中的结论还成立吗？如果成立，请给予证明；如果不成立，请说明理由；

（2）如图3，若点 $E$ 在线段 $BC$ 上，以 $BE$ 和 $BF$ 为邻边作平行四边形 $BEHF$ ， $M$ 是 $BH$ 中点，连接 $GM$ ， $AB = 3$ ， $BC = 2$ ，求 $GM$ 的最小值．

某工艺品厂设计了一款每件成本为11元的工艺品投放市场进行试销，经过市场调查，得出每天销售量 $y$ （件 $)$ 是每件售价 $x$ （元 $) (x$ 为正整数）的一次函数，其部分对应数据如下表所示：

每件售价 $x$ （元 $)$	$\dots$	15	16	17	18	$\dots$
每天销售量 $y$ （件 $)$	$\dots$	150	140	130	120	$\dots$

（1）求 $y$ 关于 $x$ 的函数解析式；

（2）若用 $w$ （元 $)$ 表示工艺品厂试销该工艺品每天获得的利润，试求 $w$ 关于 $x$ 的函数解析式；

（3）该工艺品每件售价为多少元时，工艺品厂试销该工艺品每天获得的利润最大，最大利润是多少元？

如图， $AB$ 是 $⊙ O$ 的直径，点 $C$ ，点 $D$ 在 $⊙ O$ 上， $\hat{AC} = \hat{CD}$ ， $AD$ 与 $BC$ 相交于点 $E$ ， $AF$ 与 $⊙ O$ 相切于点 $A$ ，与 $BC$ 延长线相交于点 $F$ ．

（1）求证： $AE = AF$ ．

（2）若 $EF = 12$ ， $\sin ∠ ABF = \frac{3}{5}$ ，求 $⊙ O$ 的半径．