如图,抛物线 与 轴交于 , 两点(点 在点 的左边).直线 分别交 轴, 轴于 , 两点,且除了点 之外,该直线与抛物线没有其它任何交点.
(1)求 , 两点的坐标;
(2)求 , 的值;
(3)设点 是抛物线上的动点,过点 作直线 的垂线,垂足为 ,交抛物线的对称轴于点 ,求 的最小值.并求出此时点 的坐标.

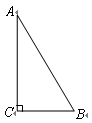
如图所示,在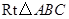 中,
中,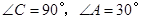 .
.
(1)尺规作图:作线段
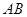 的垂直平分线
的垂直平分线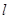 (
( 保留作图痕迹,不写作法);
保留作图痕迹,不写作法);(2)在已作的图形中,若
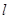 分别交
分别交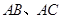 及
及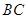 的延长线于点
的延长线于点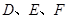 ,连接
,连接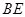 .
.
求证: .
.
如图小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长,若已知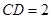 ,求
,求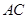 的长?
的长?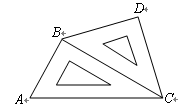
先化简,
解不等式组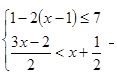 并把其解集在数轴上表示出来。
并把其解集在数轴上表示出来。
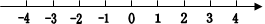 |
如图10所示,已知A点的坐标为(-1,0),点B的坐标是(9,0)以AB为直径作⊙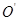 ,交y轴负半轴于点C,连接AC、BC,过A、B、C作抛物线
,交y轴负半轴于点C,连接AC、BC,过A、B、C作抛物线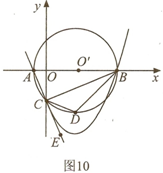
(1)求抛物线的解析式
(2)点E是AC延长线上的一点,∠BCE的平分线CD交⊙
 于点D,连结BD求BD直线的解析式
于点D,连结BD求BD直线的解析式(3)在(2)的条件下,点P是直线BC下方的抛物线上一动点,当点P运动到什么位置时,△PCD的面积是△BCD面积的
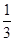 ,求此时点P的坐标
,求此时点P的坐标