某商场为提高服务质量，随机调查了50名男顾客和50名女顾客，每位顾客对该商场的服务给出满意或不满意的评价，得到下面列联表：
满意 |
不满意 |
|
男顾客 |
40 |
10 |
女顾客 |
30 |
20 |
（1）分别估计男、女顾客对该商场服务满意的概率；
（2）能否有95%的把握认为男、女顾客对该商场服务的评价有差异？
附： ．
P（ K 2≥ k） |
0.050 |
0.010 |
0.001 |
k |
3.841 |
6.635 |
10.828 |
已知函数
（I）求函数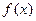
在[1，3]上的最小值；
（II）若存在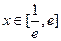
（e为自然对数的底数，且
）使不等式
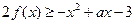成立，求实数a的取值范围
如图，正方形ADEF与梯形ABCD所在的平面互相垂直，
AB//CD，AB=AD=2，CD=4，M为CE的中点。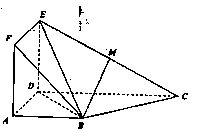
（I）求证：BM//平面ADEF；
（II）求证：平面
平面BEC；
（III）求平面BEC与平面ADEF所成锐二面角的余弦值。
已知数列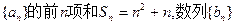
满足
且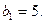
（I）求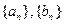
的通项公式；
（II）设数列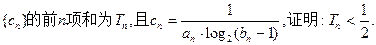
函数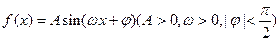
的部分图象如图所示。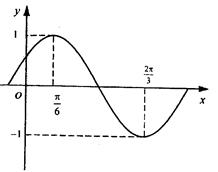
（I）求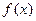
的最小正周期及解析式；
（II）设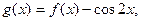
求函数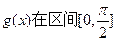
上的最大值和最小值
（本小题满分15分）
已知函数
（I）当
的单调区间；
（II）若函数
的最小值；
（III）若对任意给定的
，使得
的取值范围。