为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位: cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取次序 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
零件尺寸 |
9.95 |
10.12 |
9.96 |
9.96 |
10.01 |
9.92 |
9.98 |
10.04 |
抽取次序 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
零件尺寸 |
10.26 |
9.91 |
10.13 |
10.02 |
9.22 |
10.04 |
10.05 |
9.95 |
经计算得 x i=9.97, s 0.212, 18.439, ( x i )( i﹣8.5)=﹣2.78,其中 x i为抽取的第 i个零件的尺寸, i=1,2,…,16.
(1)求( x i, i)( i=1,2,…,16)的相关系数 r,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若| r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在( 3 s, 3 s)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)从这一天抽检的结果看,是否需对当天的生产过程进行检查?
(ⅱ)在( 3 s, 3 s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
附:样本( x i, y i)( i=1,2,…, n)的相关系数 r , 0.09.
一个袋中有大小相同的标有1,2,3,4,5,6的6个小球,某人做如下游戏,每次从
袋中拿一个球(拿后放回),记下标号.若拿出球的标号是3的倍数,则得1分,否则得 分.(Ⅰ)求拿4次至少得2分的概率; (Ⅱ)求拿4次所得分数
分.(Ⅰ)求拿4次至少得2分的概率; (Ⅱ)求拿4次所得分数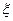 的分布列和数学期望.
的分布列和数学期望.
如图,三棱锥 中,
中,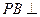 底面
底面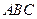 ,
,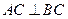 ,
, ,点
,点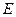 、
、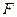 分别是
分别是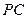 、
、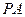 的中点.
的中点.
(Ⅰ)求证: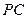 ⊥平面
⊥平面 ;(Ⅱ)求二面角
;(Ⅱ)求二面角 的大小.
的大小.

(本小题满分12分)在 中,已知内角A、B、C所对的边分别为a、b、c,向量
中,已知内角A、B、C所对的边分别为a、b、c,向量 ,
,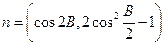 ,且
,且 。(I)求锐角B的大小;(II)如果
。(I)求锐角B的大小;(II)如果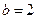 ,求
,求 的面积
的面积 的最大值。
的最大值。
(本小题满分14分)已知递增数列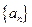 满足:
满足: ,
,
 ,且
,且 、
、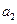 、
、 成等比数列。(I)求数列
成等比数列。(I)求数列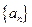 的通项公式
的通项公式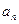 ;(II)若数列
;(II)若数列 满足:
满足: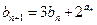
 ,且
,且 。①证明数列
。①证明数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式
的通项公式 ;②设
;②设 ,数列
,数列 前
前 项和为
项和为 ,
,
 ,
, 。当
。当 时,试比较A与B的大小。
时,试比较A与B的大小。